PCA(principal component analysis)
PCA
- 여러 변수 간에 존재하는 상관관계를 이용해 이를 대표하는 주성분(principal component)을 추출해 차원을 축소하는 기법이며, 가장 높은 분산을 가지는 데이터의 축을 찾아 이 축으로 차원을 축소하는데, 이것이 PCA의 주성분.
- 첫 번째 벡터 축 : 가장 큰 데이터 변동성을 기반으로 생성
두 번째 벡터 축 : 첫 번째 벡터 축에 직각이 되는 벡터(직교벡터)
세 번째 벡터 축 : 두 번째 벡터 축과 직각이 되는 벡터를 설정하는 방식으로 축 생성
PCA의 선형대수 관점
- 입력 데이터의 공분산 행렬을 고유값 분해하고, 이렇게 구한 고유벡터에 입력 데이터를 선형 변환하는 것
- 이 고유 벡터가 PCA의 주성분벡터로서 입력 데이터의 분산이 큰 방향을 나타냄

- 공분산c = 고유벡터 직교 행렬 * 고유값 정방 행렬 * 고유벡터 직교 행렬의 전치 행렬
즉 입력 데이터의 공분산 행렬이 고유벡터와 고유값으로 분해될 수 있으며, 이렇게 분해된 고유벡터를 이용해 입력 데이터를 선형 변환하는 방식이 PCA이다.
PCA step
1. 입력 데이터 세트의 공분산 행렬을 생성
2. 공분산 행렬의 고유벡터와 고유값을 계산
3. 고유값이 가장 큰 순으로 K개(PCA 변환 차수만큼)만큼 고유벡터를 추출
4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력 데이터를 변환
예제
- 붓꽃 데이터세트에 있는 4개의 속성을 2개의 PCA차원으로 압축해 원래 데이터 세트와 압축된 데이터 세트가 어떻게
달라지는지 비교
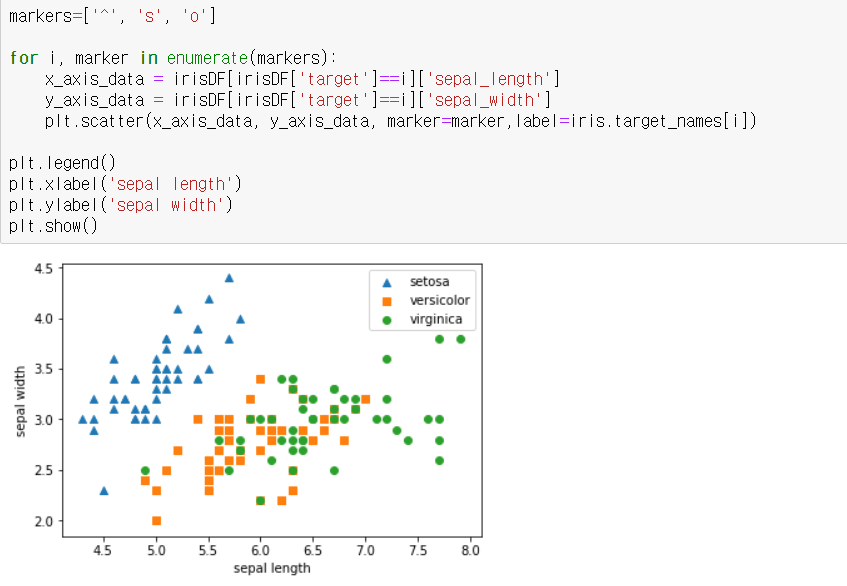
-> 붓꽃 데이터세트에 있는 4개의 속성을 2차원으로 표현하므로 두 개의 속성인 sepal length, sepal width를 각각
X축, Y축으로 해 품종 데이터 분포를 시각화
-> Versicolor와 virginica의 경우는 X축과Y축 조건만으로는 분류가 어려운 복잡한 조건임을 알 수 있음
[ PCA 변환]

-> PCA는 여러 속성의 값을 연산해야 하므로 속성의 스케일에 영향을 받기때문에 여러 속성을 PCA로 압축하기 전에 각
속성값을 동일한 스케일로 변환하는 것이 필요하여 사이킷런의 standardscaler를 이용해 원본 데이터를 변환
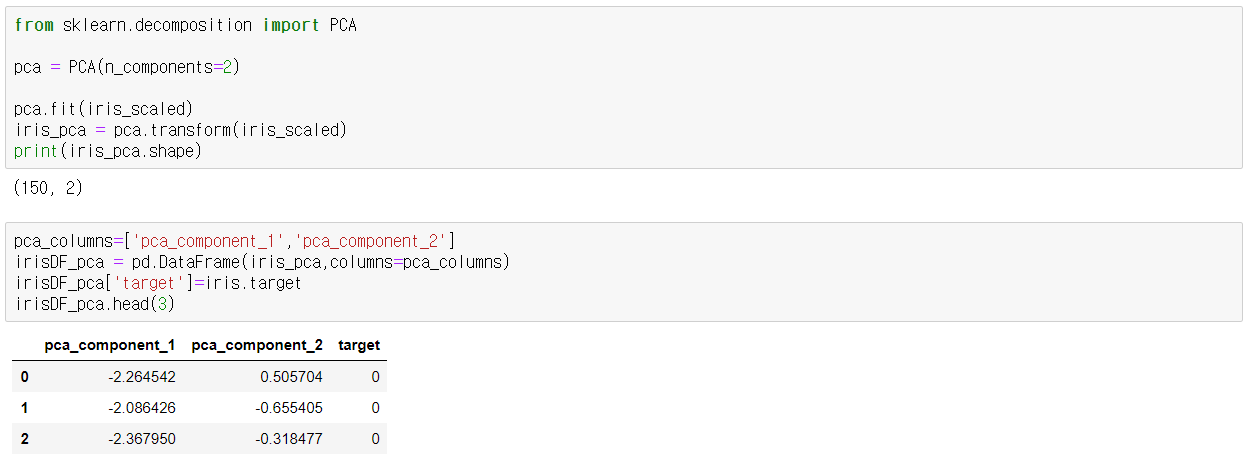
-> 원본 데이터를 PCA데이터로 PCA클래스를 이용하여 변환하였고, PCA클래스는 생성 파라미터로 n_components
( PCA로 변환할 차원의 수를 의미 )를 입력
-> transform( ) 메서드를 호출해 원본 데이터 세트를 pca 객체 변수로 반환( 150x2넘파이 행렬)
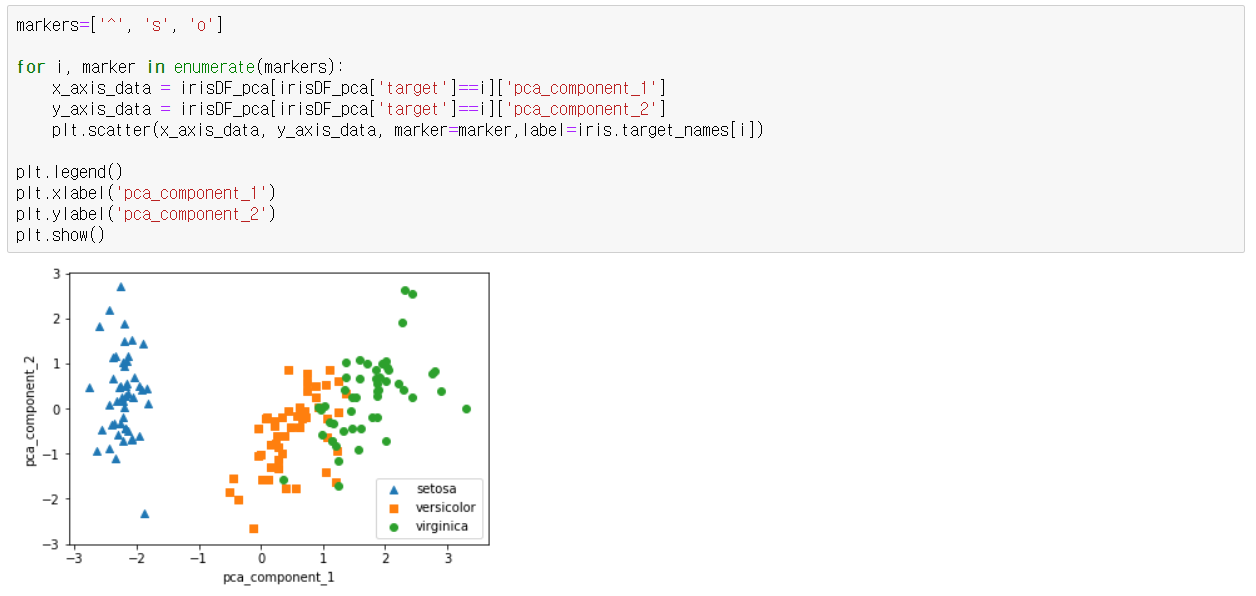
-> 원본보다 pca_component_1값을 기준으로 비교적 며왁한 구분이 가능해졌으며 이는 PCA의 첫 번째 새로운 축인
pca_component_1이 원본 데이터의 변동성을 잘 반영했다는 결과

-> explained_variance_ratio_속성을 통해 전체 변동성에서 개별 PCA 컴포넌트별로 차지하는 변동성 비율을 제공
-> PCA를 2개 요소로만 변환해도 원동 데이터의 변동성을 95% 설명가능

-> 원본보다 PCA 변환된 데이터 세트가 더 나은 예측 정확도를 나타내지만 이러한 경우는 흔하지 않음
-> PCA 변환 차원 개수에 따라 예측 성능이 떨어질 수밖에 없음
-> 붓꽃 데이터의 경우는 4개의 속성이 2개의 변환 속성이 돼도 예측 성능에 전혀 영향을 받지 않을 정도로 PCA변환이
잘 적용됐음을 의미